Represent Cauchy Distribution Using t Location-Scale
This example shows how to use the t location-scale probability distribution object to work with a Cauchy distribution with nonstandard parameter values.
Step 1. Create a probability distribution object.
Create a location-scale probability distribution object with degrees of freedom nu = 1. Specify mu = 3 to set the location parameter equal to 3, and sigma = 1 to set the scale parameter equal to 1.
pd = makedist('tLocationScale','mu',3,'sigma',1,'nu',1)
pd =
tLocationScaleDistribution
t Location-Scale distribution
mu = 3
sigma = 1
nu = 1
Step 2. Compute descriptive statistics.
Use object functions to compute descriptive statistics for the Cauchy distribution.
med = median(pd)
med = 3
r = iqr(pd)
r = 2
m = mean(pd)
m = NaN
s = std(pd)
s = Inf
The median of the Cauchy distribution is equal to its location parameter, and the interquartile range is equal to two times its scale parameter. Its mean and standard deviation are undefined.
Step 3. Compute and plot the pdf.
Compute and plot the pdf of the Cauchy distribution.
x = -20:1:20;
y = pdf(pd,x);
plot(x,y,'LineWidth',2)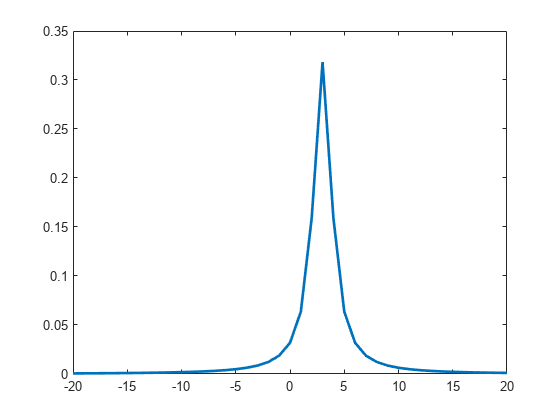
The peak of the pdf is centered at the location parameter mu = 3.
Step 4. Generate a vector of Cauchy random numbers.
Generate a column vector containing 10 random numbers from the Cauchy distribution using the random function for the location-scale probability distribution object.
rng('default'); % For reproducibility r = random(pd,10,1)
r = 10×1
3.2678
4.6547
2.0604
4.7322
3.1810
1.6649
1.8471
4.2466
5.4647
8.8874
Step 5. Generate a matrix of Cauchy random numbers.
Generate a 5-by-5 matrix of Cauchy random numbers.
r = random(pd,5,5)
r = 5×5
2.2867 2.9692 -1.7003 5.5949 1.9806
2.7421 2.7180 3.2210 2.4233 3.1394
3.5966 3.9806 1.0182 6.4180 5.1367
5.4791 15.6472 0.7558 2.8908 5.9031
1.6863 4.0985 2.9934 13.9506 4.8792
