对数正态分布
概述
对数正态分布,有时称为高尔顿分布,是一种对数服从正态分布的概率分布。当所关注的数量必须为正数时,对数正态分布才适用,因为 log(x) 仅在 x 为正数时存在。
Statistics and Machine Learning Toolbox™ 提供了几种处理对数正态分布的方法。
参数
对数正态分布使用下列参数。
| 参数 | 描述 | 支持 |
|---|---|---|
mu (μ) | 对数值的均值 | |
sigma (σ) | 对数值的标准差 |
如果 X 服从具有参数 µ 和 σ 的对数正态分布,则 log(X) 服从具有均值 µ 和标准差 σ 的正态分布。
参数估计
要对数据进行对数正态分布拟合并求出参数估计值,请使用 lognfit、fitdist 或 mle。
对于未删失数据,
lognfit和fitdist计算分布参数的无偏估计值,mle计算最大似然估计值。对于删失数据,
lognfit、fitdist、mle计算最大似然估计值。
与返回参数估计值的 lognfit 和 mle 不同,fitdist 返回拟合的概率分布对象 LognormalDistribution。对象属性 mu 和 sigma 存储参数估计值。
描述性统计量
对数正态随机变量的均值 m 和方差 v 是对数正态分布参数 µ 和 σ 的函数:
此外,您可以根据均值 m 和方差 v 计算对数正态分布参数 µ 和 σ:
概率密度函数
对数正态分布的概率密度函数 (pdf) 为
有关示例,请参阅计算对数正态分布 pdf。
累积分布函数
对数正态分布的累积分布函数 (cdf) 是
有关示例,请参阅计算对数正态分布 cdf。
示例
计算对数正态分布 pdf
假设美国四口之家的收入服从 mu = log(20,000) 且 sigma = 1 的对数正态分布。计算并绘制收入密度。
通过指定参数值创建对数正态分布对象。
pd = makedist('Lognormal','mu',log(20000),'sigma',1)
pd =
LognormalDistribution
Lognormal distribution
mu = 9.90349
sigma = 1
计算 pdf 值。
x = (10:1000:125010)'; y = pdf(pd,x);
绘制 pdf。
plot(x,y)
h = gca;
h.XTick = [0 30000 60000 90000 120000];
h.XTickLabel = {'0','$30,000','$60,000',...
'$90,000','$120,000'};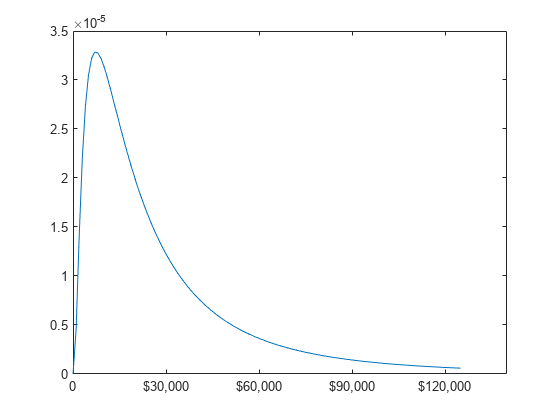
计算对数正态分布 cdf
计算均值为 mu 和标准差为 sigma 的对数正态分布在 x 中的值处计算的 cdf 值。
x = 0:0.2:10; mu = 0; sigma = 1; p = logncdf(x,mu,sigma);
绘制 cdf。
plot(x,p) grid on xlabel('x') ylabel('p')
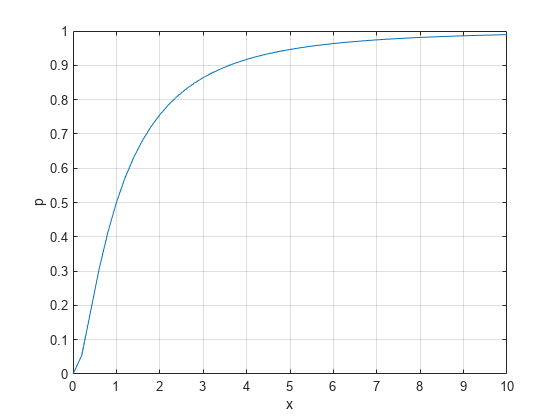
正态分布和对数正态分布之间的关系
如果 X 遵循具有参数 µ 和 σ 的对数正态分布,则 log(X) 遵循具有均值 µ 和标准差 σ 的正态分布。使用分布对象检查正态分布和对数正态分布之间的关系。
通过指定参数值创建对数正态分布对象。
pd = makedist('Lognormal','mu',5,'sigma',2)
pd =
LognormalDistribution
Lognormal distribution
mu = 5
sigma = 2
计算对数正态分布的均值。
mean(pd)
ans = 1.0966e+03
对数正态分布的均值不等于 mu 参数。对数值的均值等于 mu。通过生成随机数来确认这种关系。
从对数正态分布中生成随机数,并计算其对数值。
rng('default'); % For reproducibility x = random(pd,10000,1); logx = log(x);
计算对数值的均值。
m = mean(logx)
m = 5.0033
x 的对数的均值接近 x 的 mu 参数,因为 x 具有对数正态分布。
用正态分布拟合构造 logx 的直方图。
histfit(logx)
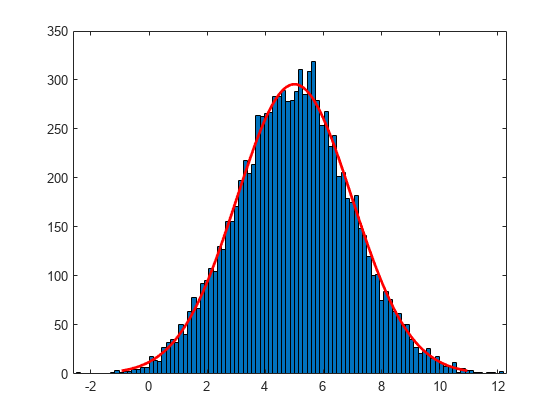
该图显示 x 的对数值呈正态分布。
histfit 使用 fitdist 对数据进行分布拟合。使用 fitdist 获得在拟合中使用的参数。
pd_normal = fitdist(logx,'Normal')pd_normal =
NormalDistribution
Normal distribution
mu = 5.00332 [4.96445, 5.04219]
sigma = 1.98296 [1.95585, 2.01083]
估计的正态分布参数接近对数正态分布参数 5 和 2。
比较对数正态分布 pdf 和伯尔分布 pdf
使用从对数正态分布生成的收入数据比较对数正态 pdf 和伯尔 pdf。
生成收入数据。
rng('default') % For reproducibility y = random('Lognormal',log(25000),0.65,[500,1]);
拟合伯尔分布。
pd = fitdist(y,'burr')pd =
BurrDistribution
Burr distribution
alpha = 26007.2 [21165.5, 31956.4]
c = 2.63743 [2.3053, 3.0174]
k = 1.09658 [0.775479, 1.55064]
在同一图窗上绘制收入数据的伯尔 pdf 和对数正态 pdf。
p_burr = pdf(pd,sortrows(y)); p_lognormal = pdf('Lognormal',sortrows(y),log(25000),0.65); plot(sortrows(y),p_burr,'-',sortrows(y),p_lognormal,'-.') title('Burr and Lognormal pdfs Fit to Income Data') legend('Burr Distribution','Lognormal Distribution')
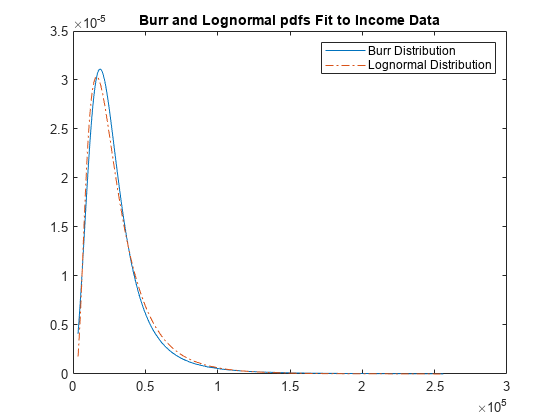
相关分布
正态分布 - 对数正态分布与正态分布密切相关。如果 X 服从具有参数 μ 和 σ 的对数正态分布,则 log(x) 服从具有均值 μ 和标准差 σ 的正态分布。请参阅正态分布和对数正态分布之间的关系。
Burr Type XII Distribution - 伯尔分布是一种灵活的分布族,可以表示多种分布形状。作为极限情况,它有许多常用的分布,如 gamma、对数正态、对数逻辑、钟形和 J 形 beta 分布(但不是 U 形)。请参阅比较对数正态分布 pdf 和伯尔分布 pdf。
参考
[1] Abramowitz, Milton, and Irene A. Stegun, eds. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. 9. Dover print.; [Nachdr. der Ausg. von 1972]. Dover Books on Mathematics. New York, NY: Dover Publ, 2013.
[2] Evans, M., N. Hastings, and B. Peacock. Statistical Distributions. 2nd ed., Hoboken, NJ: John Wiley & Sons, Inc., 1993.
[3] Lawless, J. F. Statistical Models and Methods for Lifetime Data. Hoboken, NJ: Wiley-Interscience, 1982.
[4] Marsaglia, G., and W. W. Tsang. “A Fast, Easily Implemented Method for Sampling from Decreasing or Symmetric Unimodal Density Functions.” SIAM Journal on Scientific and Statistical Computing. Vol. 5, Number 2, 1984, pp. 349–359.
[5] Meeker, W. Q., and L. A. Escobar. Statistical Methods for Reliability Data. Hoboken, NJ: John Wiley & Sons, Inc., 1998.
[6] Mood, A. M., F. A. Graybill, and D. C. Boes. Introduction to the Theory of Statistics. 3rd ed., New York: McGraw-Hill, 1974. pp. 540–541.
另请参阅
LognormalDistribution | logncdf | lognpdf | logninv | lognlike | lognstat | lognfit | lognrnd
